連載・コラム
人事データ活用入門 第6回
「t検定」で平均の差を比較する
- 公開日:2017/10/16
- 更新日:2025/04/15

今回は、新卒採用者と中途採用者の特徴、研修前後の職務遂行能力の発揮状況など、「異なるグループ間」あるいは「異なる時点間」で差を比較する際に用いる方法であるt検定についてご紹介します。
- 人事データ活用入門 第10回
- 複雑なメカニズムを解きほぐす「共分散構造分析」
- 人事データ活用入門 第9回
- 「因子分析」でアンケート項目のまとまりを発見する
- 人事データ活用入門 第8回
- 「二要因の分散分析」で職種別・業績別の仕事満足度を比較する
- 人事データ活用入門 第7回
- 「分散分析」で職種別の仕事満足度を比較する
- 人事データ活用入門 第6回
- 「t検定」で平均の差を比較する
- 人事データ活用入門 第5回
- 「重回帰分析」とは?活躍予測の例で理解する、予測力向上の方法
- 人事データ活用入門 第4回
- 因果関係を分析する一手法「回帰分析」とは
- 人事データ活用入門 第3回
- データの関係性を表せる「相関係数」と2つの落とし穴
- 人事データ活用入門 第2回
- 人事データに潜む2つの罠
- 人事データ活用入門 第1回
- 人事ビッグデータとは何モノなのか?
差の比較を行う
「新卒採用者と中途採用者、どちらが自社に適応しているかを確認したい」という問題意識があったとします。その場合、例えば以下のようなアプローチで分析を行うことができます。
(1)新卒採用者と中途採用者、双方に「あなたは、この会社で自分の能力を発揮できていますか」という項目について、リッカート形式の5件法(5点:あてはまる/4点:ややあてはまる/3点:どちらともいえない/2点:ややあてはまらない/1点:あてはまらない)でアンケートを行う
(2)アンケート結果について、新卒採用者と中途採用者、それぞれの平均を取って差を比較し、アンケート得点が高い方が適応していると考える
上記について、新卒採用者のアンケート結果の平均が3.8点、中途採用者のアンケートの平均が2.2点という結果が得られたとします。この場合、皆さんは「新卒採用者の方が、アンケートの得点が高い」と考えるでしょうか。それとも、「この結果だけでは、アンケートの得点が高いとはいえない」と考えるでしょうか。
第1の問題:サンプル数が少ない場合の平均の不安定さ
単純にアンケートの得点を比較することには、2つの問題があります。第1の問題は、「サンプル数(回答者など、データにおける観測対象の数)が少ない場合に平均が不安定になってしまうこと」です。
図表1をご覧ください。

もとの回答者が新卒採用者、中途採用者それぞれ「50名ずつの場合」、「5名ずつの場合」に、表のように同じ条件の回答者が増えたとします。
「50名ずつの場合」は、回答者が増える前後のいずれでも、「新卒採用者の平均>中途採用者の平均」となっています。しかし、「5名ずつの場合」では、回答者が増える前後で新卒採用者と中途採用者の平均の大小関係が逆転してしまいます。
このような例は極端なものですが、サンプル数が少ない場合、新たなサンプルの回答結果が加わることで、平均が容易に変動します。それによって、差の有無、あるいは大小関係の逆転が容易に起こります。
よって、差の確認を行う場合には、「サンプル数」を無視することは危険なことといえます。
第2の問題:ばらつきの影響
第2の問題は、「ばらつきの影響」です。図表2をご覧ください。
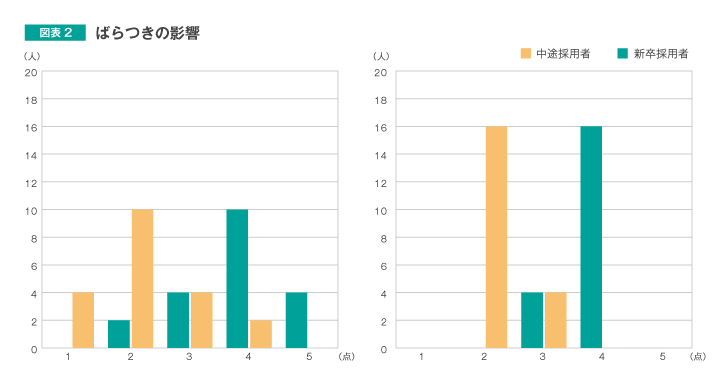
左図も右図も、「新卒採用者と中途採用者のデータ各20名分」「新卒採用者の平均は3.8点、中途採用者の平均は2.2点」というデータです。すなわち、新卒採用者と中途採用者の2群の平均の差は、左右どちらの図も変わりません。
しかし、感覚的には、右図では2群の間に明確な違いがありそうに見え、一方の左図では、2群が重なり合っていて右図ほど明確な違いがあるようには見えないのではないでしょうか。
実際、データのばらつきを表す指標である標準偏差は、左図が0.89点、右図が0.41点と大きく異なっています。つまり、右図の方が、左図よりもデータの重なりが少ないわけです。平均の差が同じでも、ばらつきが違えば、2群の間の差があるかどうかの判断も異なってきます。
よって、差の確認を行う場合には、「ばらつきの影響」を無視するのも危険なことといえます。
t検定を利用する
このように、平均の差を比較する場合に、上記2つの問題に対処する方法がt検定です。t検定はExcelでも行うことができるので、ここではその結果を記載します。
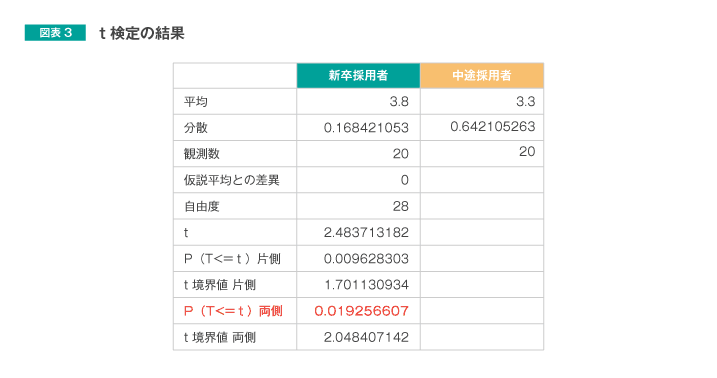
「新卒採用者、中途採用者の間に差がある」ことを確認するためにチェックする指標は、赤字の「P(T<=t) 両側」あるいは「P(T<=t) 片側」です。一般的には、p値(有意確率)と呼ばれるものです。この値が0.05未満の場合、「差がある」と考えます。
なお、「新卒採用者と中途採用者」について、どちらの得点が高いか明確な仮説がない場合は、
「P(T<=t) 両側」の値を利用します。一方、どちらの得点が高いか明確な仮説がある場合には「P(T<=t) 片側」の値を利用します。
ちなみに、「P(T<=t) 両側」「P(T<=t) 片側」はいずれも表中の「t」の値(t値)をもとに算出される値であり、t値が大きくなるほど小さくなります。
また、「P(T<=t) 両側」の値は「P(T<=t) 片側」の2倍となるため、「P(T<=t) 両側」の方が0.05未満の値を取りにくくなります。すなわち、「差がある」という結果が出づらくなります。本来は、検証したい仮説に応じてどちらの値に着目するかを事前に決めることが望ましいのですが、どちらを使うか悩む場合は「P(T<=t) 両側」を使うことが推奨されることが多いようです。
2つのt検定を使い分ける
今回の自社内の「新卒採用者と中途採用者」の比較の場合、新卒採用者と中途採用者はそれぞれ異なった人になります。このようなデータの得点の比較に使うのは、「対応のないt検定」と呼ばれる検定方法です。よって、図表3は「対応のないt検定」の分析結果です。Excelでt検定を分析ツールで行う場合は、「t検定:分散が等しくないと仮定した2標本による検定」を用います。
※事前に2つのグループの分散が等しいか否かを確認し、等しい場合は「t検定:等分散を仮定した2標本による検定」を用い、等しくない場合に「t検定:分散が等しくないと仮定した2標本による検定」を用いるという方法もあるのですが、一般的な統計的仮説検定では「分散が等しい」ということは示せないため、いずれの場合も「t検定:分散が等しくないと仮定した2標本による検定」を用いるという考え方が近年あります。実務上の簡便性のため、今回はそのスタンスにのっとっています。
一方で、研修前後の職務遂行能力の比較の場合は、同一の人材の研修前後の職務遂行能力を比較することになります。このように同一の回答者グループの2時点のデータを比較する場合に用いるのは、「対応のあるt検定」です。こちらもExcelで分析を行うことができます。分析ツールでは、「t検定:一対の標本による平均の検定」を用います。分析結果は、図表4です。
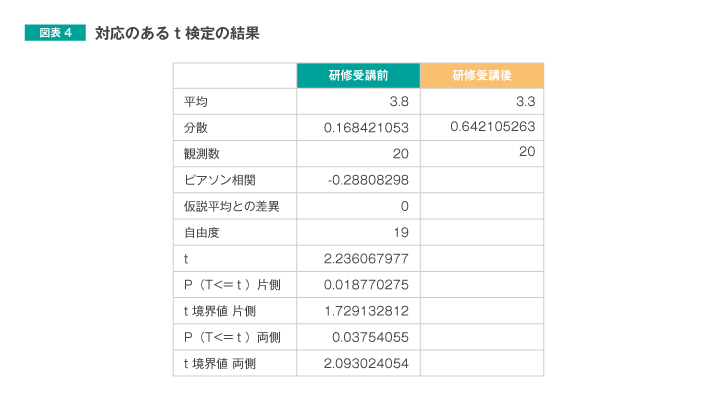
値の読み取り方、解釈は、「対応のないt検定」の場合と同様です。
t検定の留意点
まずt検定は、2つのグループの差の比較を行うものです。3つ以上のグループの差の比較を行うためには、「分散分析」という手法を用いる必要があります。分散分析については、次回ご紹介します。
また、やや専門的になりますが、t検定は「差がないとはいえない」ということを証明することによって「差がある」ということを示す方法です。手法の性質上、データ数が増えると「P(T<=t) 両側」「P(T<=t) 片側」の値が小さくなり、小さな差であっても「差がある」という結論が得られやすくなります。しかしこのことは、「実質的に意味がある差」があるということとは必ずしも一致しません。例えば、「新卒採用者の方が中途採用者よりアンケートの得点が0.01点高い」という場合、その差にはほとんど実質的に意味がないと感じられるのではないでしょうか。よって、t検定を行う際には、「実質的に意味がある差はどの程度なのか」ということも同時に考えることが必要です。
なお、t検定は比較に用いた変数の影響のみを確認する方法です。よって、その他の変数の影響を統制することができません。例えば、新卒採用者と中途採用者では、性別や職種に偏りがあるかもしれませんので、実は「差がある」という結果は、その偏りによって生じているかもしれません。
このように、「差を生み出し得る変数がいくつかあり、それがデータ化されている」場合は、次回ご紹介する分散分析や、前回ご紹介した重回帰分析などを用いることによって、それらの変数を統制する必要があります。
t検定は元来、さまざまな要因を統制する「実験」で用いられる手法なので、上記のような限界がありますが、平均の差の比較を行う際に使いやすい手法の1つなので、ぜひ留意点と共に、使用方法を覚えておいていただければと思います。
・t検定を利用した研究例はこちら
管理者適性アセスメント追跡調査2011 今日の環境下で昇進するマネジャーの要件
執筆者

技術開発統括部
研究本部
研究主幹
入江 崇介
2002年HRR入社。アセスメント、トレーニング、組織開発の商品開発・研究に携わり、現在は人事データ活用や、そのための測定・解析技術の研究に従事する。
日本学術会議協力学術研究団体人材育成学会常任理事。一般社団法人ピープルアナリティクス&HRテクノロジー協会上席研究員。昭和女子大学非常勤講師。新たな公務員人事管理に関する勉強会委員。
- 人事データ活用入門 第10回
- 複雑なメカニズムを解きほぐす「共分散構造分析」
- 人事データ活用入門 第9回
- 「因子分析」でアンケート項目のまとまりを発見する
- 人事データ活用入門 第8回
- 「二要因の分散分析」で職種別・業績別の仕事満足度を比較する
- 人事データ活用入門 第7回
- 「分散分析」で職種別の仕事満足度を比較する
- 人事データ活用入門 第6回
- 「t検定」で平均の差を比較する
- 人事データ活用入門 第5回
- 「重回帰分析」とは?活躍予測の例で理解する、予測力向上の方法
- 人事データ活用入門 第4回
- 因果関係を分析する一手法「回帰分析」とは
- 人事データ活用入門 第3回
- データの関係性を表せる「相関係数」と2つの落とし穴
- 人事データ活用入門 第2回
- 人事データに潜む2つの罠
- 人事データ活用入門 第1回
- 人事ビッグデータとは何モノなのか?
おすすめコラム
Column
関連する
無料セミナー
Online seminar
サービスを
ご検討中のお客様へ
- サービス資料・お役立ち資料
- メールマガジンのご登録をいただくことで、人事ご担当者さまにとって役立つ資料を無料でダウンロードいただけます。
- お問い合わせ
- 貴社の課題を気軽にご相談ください。最適なソリューションをご提案いたします。
- 無料オンラインセミナー
- 人事領域のプロが最新テーマ・情報をお伝えします。質疑応答では、皆さまの課題推進に向けた疑問にもお答えします。
- 無料動画セミナー
- さまざまなテーマの無料動画セミナーがお好きなタイミングで全てご視聴いただけます。
- 電話でのお問い合わせ
-
0120-878-300
受付/8:30~18:00/月~金(祝祭日を除く)
※お急ぎでなければWEBからお問い合わせください
※フリーダイヤルをご利用できない場合は
03-6331-6000へおかけください
- SPI・NMAT・JMATの
お問い合わせ -
0120-314-855
受付/10:00~17:00/月~金(祝祭日を除く)













