データの関係性を表せる「相関係数」と2つの落とし穴

2023年1月30日更新

人事業務を行うなかで、「採用時の適性検査の結果と、入社後の業績との関係は？」「1人の管理職が管理するメンバーの数と、メンバーの満足度との関係は？」「年齢とモチベーションとの関係は？」など、さまざまな「関係性」に興味をもたれたり、説明を求められたりする方も多いのではないでしょうか。
そして、そのデータから発見・確認された「関係性」に基づいて、施策を打つ対象を決定したり、施策の内容を見直したりすることもあると思います。

昨今は人事業務においてもデータを活用した取り組みが一気に増えており、活用の仕方や考え方についてご相談をいただくことも増えてきました。

今回は、「データの関係性」を確認するための指標である「相関係数」と、その留意点についてご紹介します。

※人事データの活用についてはこちらのコラムもご参考ください。
人事になったら知っておきたい10のこと　～2022人事トレンド編～　第2回
人事データ活用とアセスメント

目次

まずは見える化してみる

データの性質によって、使える手法が異なる

データの関係性を数値で表す「相関係数」

「極端な値」に注意

「非線形の関係」があっても、相関係数はゼロ

散布図を描くことが大切

まずは見える化してみる

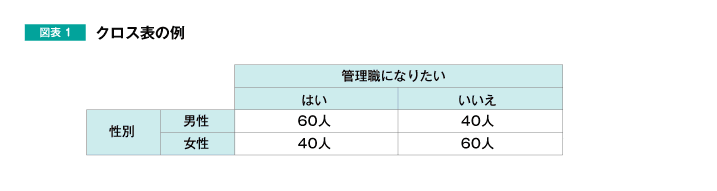
例えば、「管理職になりたいという意欲は、性別によって異なるのか」という、「性別と管理職志向の関係」を分析する場合、アンケートなどをとり、その結果を基に、図表1のようなクロス表で表すことができます。

また、「売り上げがよいメンバーほど、残業をしているのか」という、「月間の残業時間と売り上げの関係」を分析する場合、勤怠情報と売り上げ情報を基に、図表2のような散布図で表すことができます。

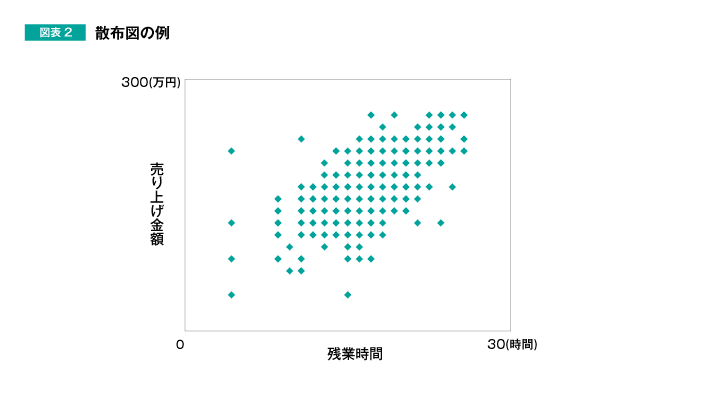
しかし、クロス表や散布図を作成しただけでは、「性別と管理職指向の関係」「月間の残業時間と売り上げの関係」の有無は、「なんとなく」は分かりますが、「どの程度の強さか」が分かりません。

データの性質によって、使える手法が異なる

ところで、このようなクロス表と散布図は、どのようにして使い分ければよいのでしょうか。
使い分けの基準として参考になるのは、図表3の「尺度水準（※1）」*という考え方です。

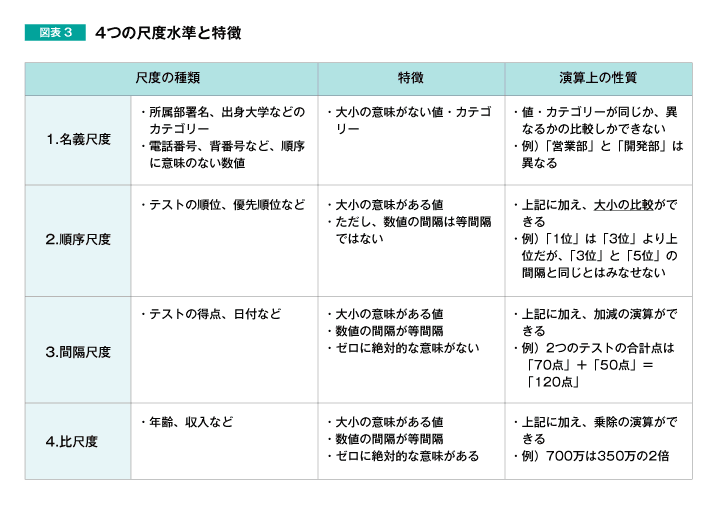
「1.名義尺度」「2.順序尺度」は、間隔に意味がない数値なので、クロス表を作成することは問題ありませんが、散布図を作成すべきではありません。なぜならば、X軸とY軸の間隔が意味のないものになってしまうからです。

一方で、「3.間隔尺度」「4.比尺度」は、間隔に意味がある数値なので、クロス表・散布図のいずれを作成しても問題がありません。

なお、性格検査やアンケートでよく用いられる「あてはまる／どちらかといえばあてはまる／どちらともいえない／どちらかといえばあてはまらない／あてはまらない」という選択肢を用いる方法は、「リッカート法」といわれ、「あてはまる＝5点／どちらかといえばあてはまる＝4点／どちらともいえない＝3点／どちらかといえばあてはまらない＝2点／あてはまらない＝1点」のように、数値化して分析に用いられることがあります。
主に心理学では、このとき、「1と2の差」「2と3の差」「3と4の差」「4と5の差」は等間隔とみなし、「3.間隔尺度」として用いることが少なくありません。それによって、集団の平均値などが扱えるようになっているのです。

データの関係性を数値で表す「相関係数」

尺度水準によって、データの関係性を分析する方法も変わってきます。今回は、Excelでも簡単に分析することができる、2つの変数の関係性を示す「相関係数」についてご紹介します。

実は、相関係数にはいくつかの種類があるのですが、「月間の残業時間と売り上げの関係」「年齢と年収の関係」など、「3.間隔尺度」「4.比尺度」に対して一般的に用いられるのは、「ピアソンの積率相関係数」というものです。Excelであれば、分析ツールやcorrelという関数を使うことで求めることができます。ちなみに、ピアソンの積率相関係数は「1.名義尺度」「2.順序尺度」に対しては利用できません。
以降では、簡便化のために、ピアソンの積率相関係数のことを「相関係数」とします。

この相関係数は、－1～1の間の値をとります。絶対値が1に近いほど、2つの変数の関係性が強いことを示します。相関係数の大きさと散布図の関係を示すと、図表4のようになります。

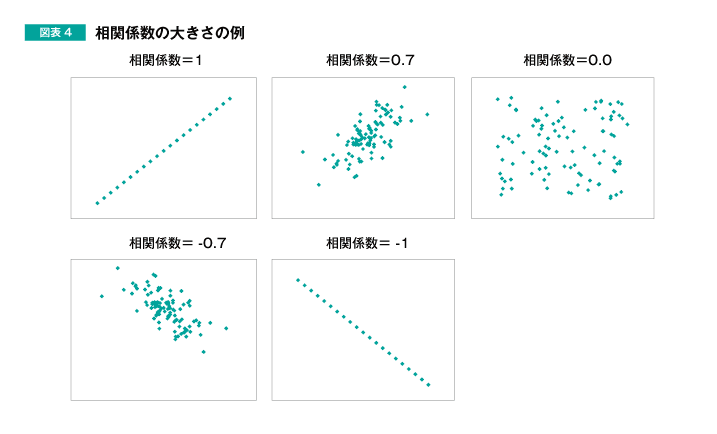
相関係数は、「一方が大きくなれば、他方も大きくなる」場合はプラスの値になります。逆に、「一方が大きくなれば、他方が小さくなる」場合はマイナスの値になります。
また、2つの変数の関係が直線に近いほど絶対値の大きな値をとり、ばらばらになるほどゼロに近い絶対値の小さな値をとります。

散布図を観察するだけでは、「なんとなく大きい」「なんとなく小さい」としか読み解けなかった2つの変数の関係性が、相関係数を利用することで定量化することができるので、相関係数は非常に便利な値です。
しかし、相関係数には特有の癖があるので、それに注意が必要です。
今回は、2つの注意点をご紹介します。

「極端な値」に注意

1つ目の注意点は、「相関係数は、極端な値（以下、外れ値）の影響を受ける」ということです。図表5をご覧ください。

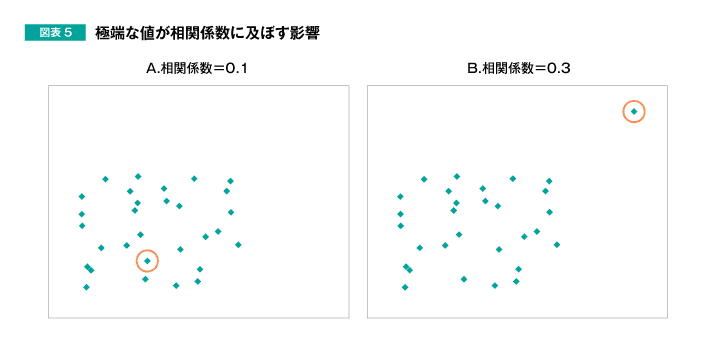
図表5は30個のデータからなる散布図ですが、実は「A.相関係数＝0.1」と「B.相関係数＝0.3」は、赤色で囲った1つの値だけが異なるデータなのです。この1つの外れ値によって、相関係数が異なってしまうことが確認できます。なお、他の29個の変数だけを用いて相関係数を求めると、0.1となります。

実際、このような現象は起きやすいものです。例えば、年齢と給与の関係を分析した際に、1人だけ「年齢が高く、給与が高い社長」がいたとすると、他の従業員においては「年齢と給与にはほとんど関係がない」にもかかわらず、「年齢と給与にはある程度関係がある」という結果になってしまいます。

「非線形の関係」があっても、相関係数はゼロ

2つ目の注意点は、「曲線関係など、非線形の関係があっても、相関係数にはそれが表れない」ことです。図表6をご覧ください。

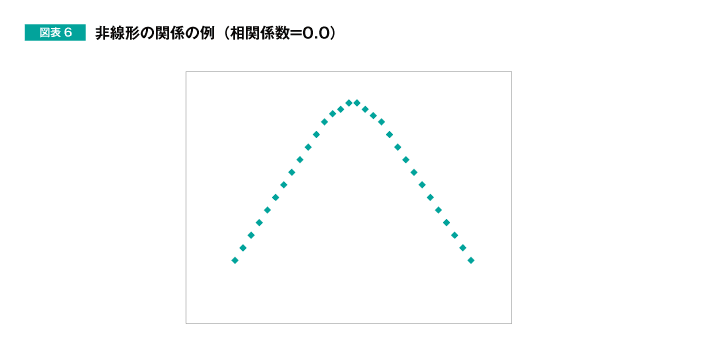
こちらの散布図を見ると、縦軸と横軸の2つの変数の間には、明らかに「2次曲線」の関係性があることが見て取れます。しかし、この場合の相関係数はゼロになります。

「ストレスは、高すぎても低すぎてもパフォーマンスに悪影響を及ぼす」というようなことが言われることがありますが、そのような関係性を検証するには相関係数は不十分な指標であり、相関係数を求めるだけでは、「本来、分かったら役に立つ」発見を見逃してしまう可能性があるのです。

散布図を描くことが大切

例えば、図表7のように、「総合満足度と、さまざまな職場要因との関係性」を確認するような場合、相関係数を一覧化すれば、どの要因の関係性が強いか弱いかを簡単に読み取ることができます。

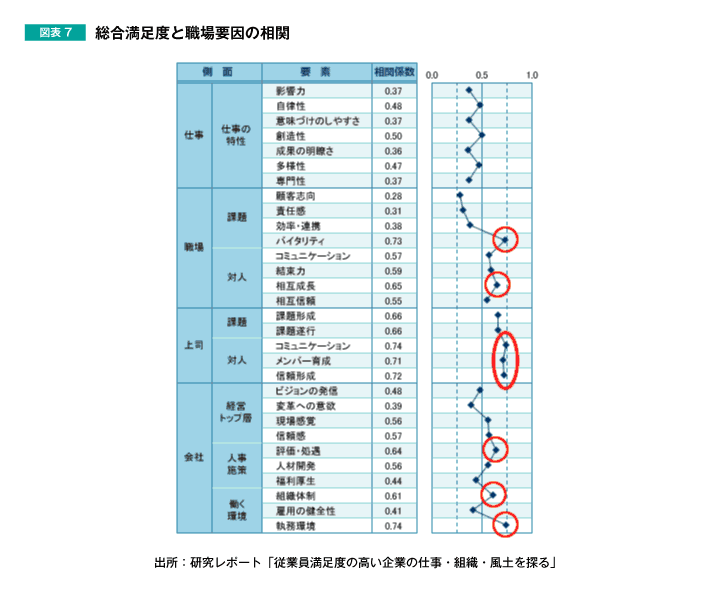
このように、相関係数は非常に便利な指標です。
一方で、「相関係数は、外れ値の影響を受ける」「曲線関係など、非線形の関係があっても、相関係数にはそれが表れない」といった落とし穴がある指標でもあります。

では、このような問題はどのようにすれば防げるのでしょうか。
そのための方法は、図表2の「散布図」を描くことです。

それによって外れ値が確認されれば、それを除いて分析するという対処ができます。また、曲線的な関係が確認されれば、別途その強さを確認する方法で分析を行うことができます。

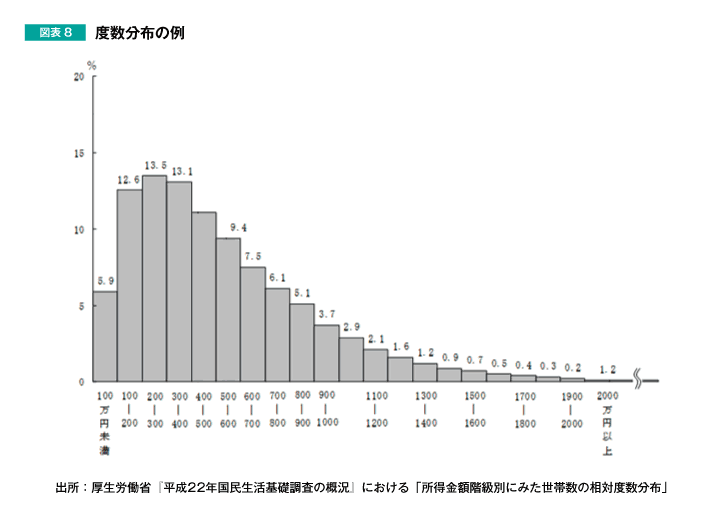
特に、分析に使うデータの性質がよく分からない場合には、散布図を書く前に、まずは図表8のような度数分布を確認するなど、一つひとつのデータの性質を確認することが大切です。そして、2つのデータを組み合わせた関係性の分析の際には、散布図を確認することが大切になります。

複雑な統計解析の手法がさまざまありますが、まずはこのような「基本的なステップ」を欠かさないよう、ぜひご注意ください。

今回は、変数の関係性を検証するための基本的な方法である「相関」についてご紹介しました。
次回は、データの関係性を確認するための、より応用的な方法をご紹介したいと思います。

引用
※1：*S. S. Stevens (1946), “On the Theory of Scales of Measurement, ” Science 103(2684) : 677-680
※2：厚生労働省「所得金額階級別にみた世帯数の相対度数分布」