連載・コラム
人事データ活用入門 第5回
「重回帰分析」とは?活躍予測の例で理解する、予測力向上の方法
- 公開日:2017/08/07
- 更新日:2025/04/15
前回は、因果関係に基づく予測に用いる分析方法として、「回帰分析」をご紹介しました。(「回帰分析で因果関係を分析する」)今回は、予測力を高めるためにより多くの変数を用いる方法である「重回帰分析」と、その利用時の留意点をご紹介します。
- 人事データ活用入門 第10回
- 複雑なメカニズムを解きほぐす「共分散構造分析」
- 人事データ活用入門 第9回
- 「因子分析」でアンケート項目のまとまりを発見する
- 人事データ活用入門 第8回
- 「二要因の分散分析」で職種別・業績別の仕事満足度を比較する
- 人事データ活用入門 第7回
- 「分散分析」で職種別の仕事満足度を比較する
- 人事データ活用入門 第6回
- 「t検定」で平均の差を比較する
- 人事データ活用入門 第5回
- 「重回帰分析」とは?活躍予測の例で理解する、予測力向上の方法
- 人事データ活用入門 第4回
- 因果関係を分析する一手法「回帰分析」とは
- 人事データ活用入門 第3回
- データの関係性を表せる「相関係数」と2つの落とし穴
- 人事データ活用入門 第2回
- 人事データに潜む2つの罠
- 人事データ活用入門 第1回
- 人事ビッグデータとは何モノなのか?
重回帰分析とは
図表1のように、複数の変数が1つの変数に及ぼす影響を分析する方法が「重回帰分析」です。
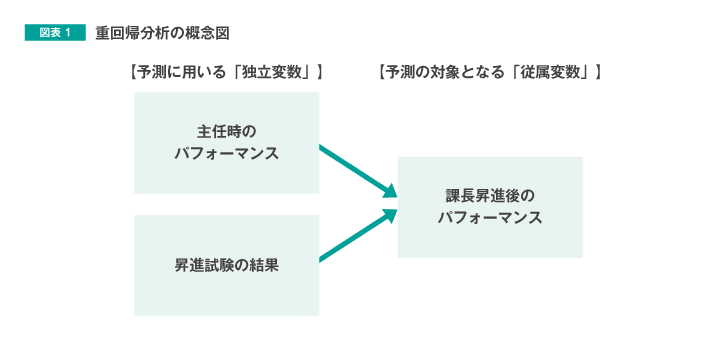
図表1の例では、予測に用いる独立変数の数は2つですが、「課長昇進後のパフォーマンス」の予測に用いることができる変数(例:入社時の適性検査の結果、資格の有無、研修受講履歴 など)が他にもあれば、3つ以上の独立変数を用いて分析を行うことができます。
重回帰分析の結果を読み取る
まず、分析に用いたデータについてご説明します。今回分析に用いたのは、第4回「回帰分析で因果関係を分析する」)で用いたデータに、「昇進試験の結果」を追加したものです。
「『課長昇進後のパフォーマンス』を従属変数、『主任時のパフォーマンス』と『昇進試験の結果』を独立変数とした重回帰分析」のExcelでの分析結果は、図表2の上の表です。
比較のために、前回実施した、「『課長昇進後のパフォーマンス』を従属変数、『主任時のパフォーマンス』を独立変数とした回帰分析」の結果を下に併記しています。
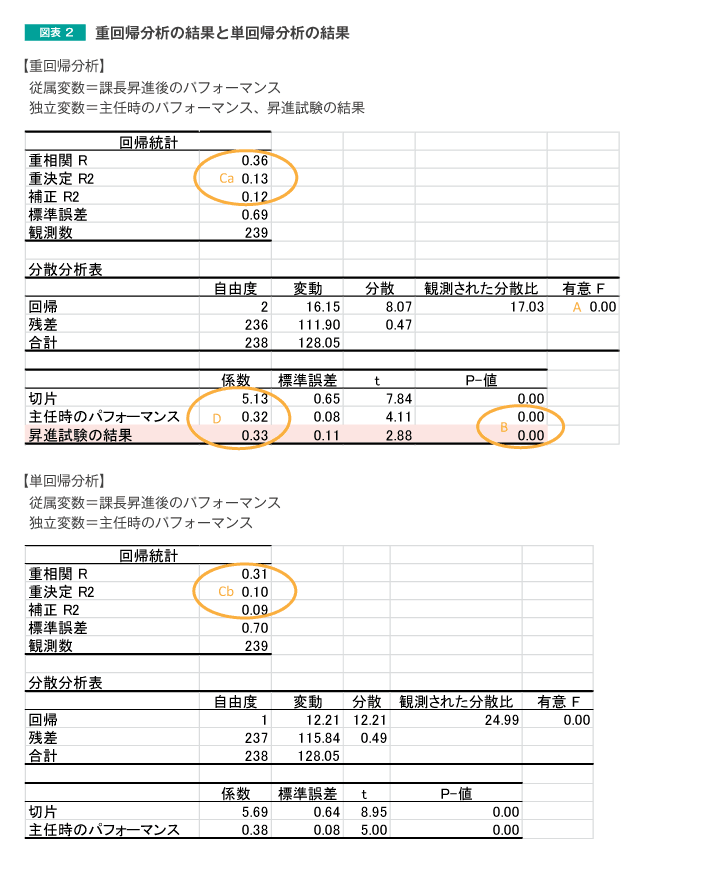
上下を比較すると、今回追加されているのは「昇進試験の結果」の行のみです。その他の部分は、分析結果の数値は異なりますが、要素としての差はありません。
では、上の重回帰分析の結果を解釈していきます。
まず、単回帰分析同様、「A:有意F」の値を確認します。この値が0.05未満であれば、統計的検定の結果、分析結果は確からしいと解釈することができます。
続いて、偏回帰係数について確認をします。前回は省略しましたが、今回は「B: P-値」を確認します。この値は、偏回帰係数の値が統計的に有意であるかを判断するための指標です。この値が0.05未満であれば、偏回帰係数の値が統計的に有意であると解釈することができます。今回の分析では、単回帰分析で用いた「主任時のパフォーマンス」だけでなく、「昇進試験の結果」も統計的に有意であることが確認できます。
では、「課長昇進後のパフォーマンスの予測」について、「昇進試験の結果」を加えたことで、精度は向上したのでしょうか。その確認は、重回帰分析・単回帰分析の予測力を示す重相関R、重決定R2、補正R2について、CaとCbの差を比較することで行うことができます。今回の分析では、いずれの値も大きくなっているため、予測力が高くなったと考えることができます。
なお、重相関Rと重決定R2は、独立変数の数を増やすと、それだけで高くなる値です。分析に用いたデータへのあてはまりを確認するためには有効な指標ですが、回帰分析の結果を予測に用いるために新たな独立変数を追加した意義の有無については、「補正R2(自由度調整済み重決定係数)」の値が大きくなっているかを重視して確認します。
重回帰分析の結果に基づく予測
では、重回帰分析の結果に基づき、「課長昇進後のパフォーマンス」を「主任時のパフォーマンス」と「昇進試験の結果」で予測するための方法をご紹介します。
予測のための数式の考え方は単回帰分析の場合と同様で、図表2の「D:係数」を用いて、
課長昇進後のパフォーマンス=5.13+0.32 × 主任時のパフォーマンス+0.33×昇進試験の結果
という数式を立て、主任時のパフォーマンスと昇進試験の結果を代入することによって、課長昇進後のパフォーマンスを予測することができます。
重回帰分析実施時の留意点
今回の分析結果から、重回帰分析を用いて独立変数の数を増やすことによって、予測力を高められることを確認しました。では、単純に予測のために用いる独立変数の数を増やせば、予測力は高まるのでしょうか。実は、必ずしもそうとは言い切れません。
図表3で、図表2の重回帰分析に用いたデータの独立変数間の相関係数を確認してみましょう。
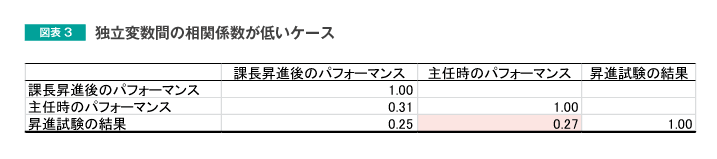
独立変数である「主任時のパフォーマンス」と「昇進試験の結果」の相関係数に着目すると、その値は0.27となっており、それほど高い値にはなっていません。このような場合、重回帰分析の結果は、安定したものとなり、独立変数の追加によって、予測力が向上することが期待できます。
では、独立変数間の相関係数が高い場合はどうなるでしょうか。図表4の場合、独立変数の間の相関係数は0.77と高い値になっています。なお、「課長昇進後のパフォーマンス」とそれぞれの独立変数の相関係数は、図表3と図表4ではほぼ同じ値となっています。

図表4のデータに対する重回帰分析の結果を図表5で確認してみましょう。上が図表4のデータに対する重回帰分析の結果、下が図表3のデータに対する重回帰分析の結果(図表2の上の図表と同様)です。
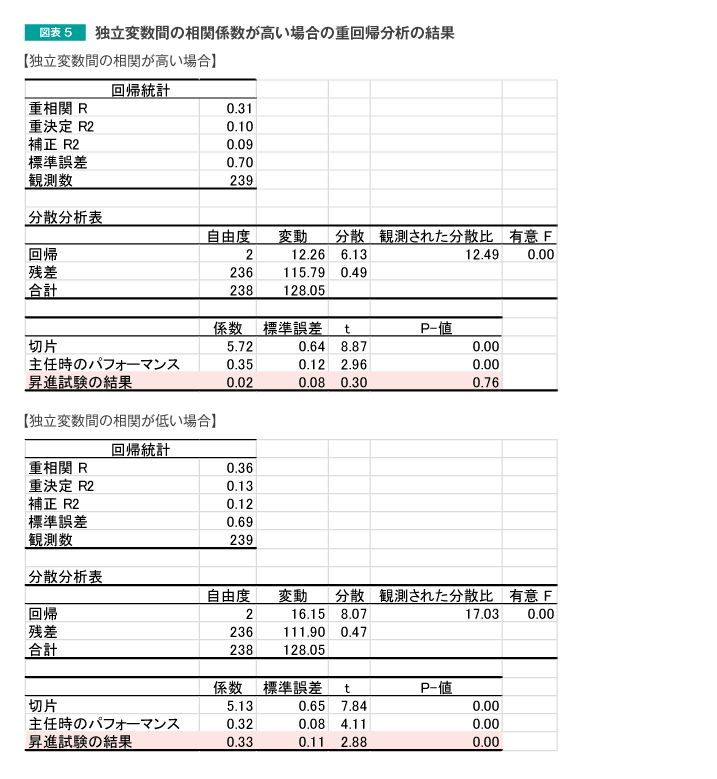
特に網かけしている部分に着目していただくと、独立変数間の相関係数が高い場合、昇進試験の結果に対するP-値は0.76となっており、こちらは課長昇進後のパフォーマンスを予測するためには、有効ではない変数となっています。
また、図表4のデータに対する重回帰分析の結果と、単回帰分析の結果とを比較した図表6をご確認ください。
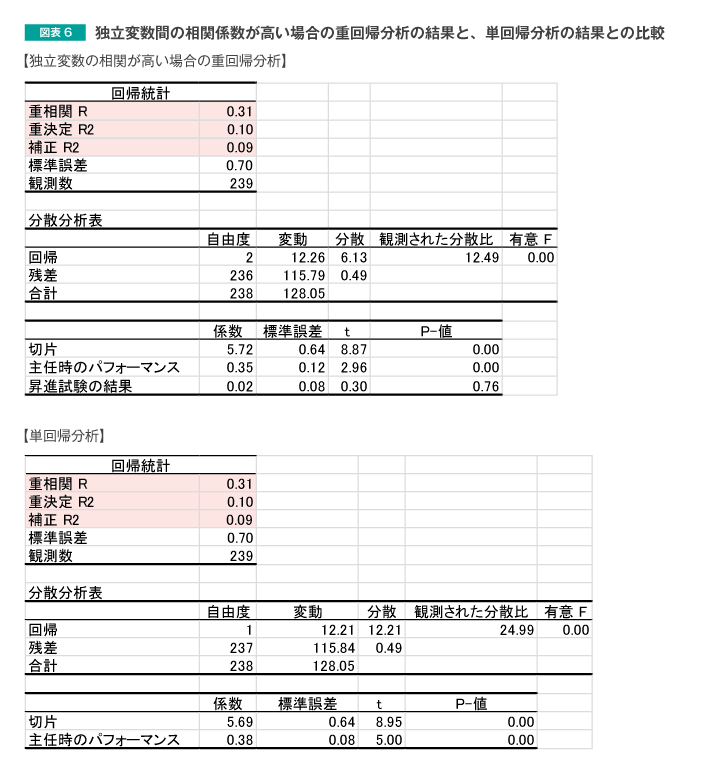
網かけ部分を確認すると、重回帰分析の結果は単回帰分析の結果と比較して、わずかではありますが、重相関Rと重決定R2は高くなっています。しかし、補正R2の値は低くなっています。すなわち、独立変数を追加したことによって、かえって予測力が下がったという結果になっています。
このような現象は、独立変数間の相関係数が高い場合に生じる「多重共線性の問題」と呼ばれており、重回帰分析を行う際に注意しなくてはならない点です。このような場合は、重回帰分析の結果は不安定なものになります。
多重共線性の問題を避けるためには、重回帰分析を行う前に、事前に相関係数を確認することが有効な方法です。
独立変数間の相関係数が高い場合には、一方の変数を分析に用いない、あるいは2つの変数の合成得点を分析に用いるなどすることによって、多重共線性の問題を回避することができます。
予測の精度を高めるためにさまざまな変数を重回帰分析に取り込んだ結果、分析結果が不安定になってしまっては、本末転倒ですので、この点には十分ご留意ください。
おわりに
重回帰分析では、標準化偏回帰係数を用いることによって複数の独立変数のなかでより予測に強い影響を及ぼすものを確認したり、交互作用を確認することによって複数の独立変数の組み合わせの効果を確認したりなど、より応用的な分析を行うこともできます。これらについてより深い理解をしたい方、応用例を知りたい方は、以下に挙げた文献を参考にしてください。
・大湾秀雄『日本の人事を科学する 因果推論に基づくデータ活用』(日本経済新聞出版社、2017年)
・豊田秀樹『もうひとつの重回帰分析』(東京図書、2017年)
・中室牧子、 津川友介『「原因と結果」の経済学―データから真実を見抜く思考法』(ダイヤモンド社、2017年)
次回は、職場別、職種別など属性別の特徴の比較などで利用する、「差の検定」についてご紹介します。
・重回帰分析を使用した研究例はこちら
「新任管理職の適応に影響を及ぼす要因」
https://www.recruit-ms.co.jp/research/study_report/0000000580/
執筆者

技術開発統括部
研究本部
研究主幹
入江 崇介
2002年HRR入社。アセスメント、トレーニング、組織開発の商品開発・研究に携わり、現在は人事データ活用や、そのための測定・解析技術の研究に従事する。
日本学術会議協力学術研究団体人材育成学会常任理事。一般社団法人ピープルアナリティクス&HRテクノロジー協会上席研究員。昭和女子大学非常勤講師。新たな公務員人事管理に関する勉強会委員。
- 人事データ活用入門 第10回
- 複雑なメカニズムを解きほぐす「共分散構造分析」
- 人事データ活用入門 第9回
- 「因子分析」でアンケート項目のまとまりを発見する
- 人事データ活用入門 第8回
- 「二要因の分散分析」で職種別・業績別の仕事満足度を比較する
- 人事データ活用入門 第7回
- 「分散分析」で職種別の仕事満足度を比較する
- 人事データ活用入門 第6回
- 「t検定」で平均の差を比較する
- 人事データ活用入門 第5回
- 「重回帰分析」とは?活躍予測の例で理解する、予測力向上の方法
- 人事データ活用入門 第4回
- 因果関係を分析する一手法「回帰分析」とは
- 人事データ活用入門 第3回
- データの関係性を表せる「相関係数」と2つの落とし穴
- 人事データ活用入門 第2回
- 人事データに潜む2つの罠
- 人事データ活用入門 第1回
- 人事ビッグデータとは何モノなのか?
おすすめコラム
Column
関連する
無料セミナー
Online seminar
サービスを
ご検討中のお客様へ
- お役立ち情報
- メールマガジンのご登録をいただくことで、人事ご担当者さまにとって役立つ資料を無料でダウンロードいただけます。
- お問い合わせ・資料請求
- 貴社の課題を気軽にご相談ください。最適なソリューションをご提案いたします。
- 無料オンラインセミナー
- 人事領域のプロが最新テーマ・情報をお伝えします。質疑応答では、皆さまの課題推進に向けた疑問にもお答えします。
- 無料動画セミナー
- さまざまなテーマの無料動画セミナーがお好きなタイミングで全てご視聴いただけます。
- 電話でのお問い合わせ
-
0120-878-300
受付/8:30~18:00/月~金(祝祭日を除く)
※お急ぎでなければWEBからお問い合わせください
※フリーダイヤルをご利用できない場合は
03-6331-6000へおかけください
- SPI・NMAT・JMATの
お問い合わせ -
0120-314-855
受付/10:00~17:00/月~金(祝祭日を除く)










 動画セミナーだからいつでもどこでも視聴可能
動画セミナーだからいつでもどこでも視聴可能
 メルマガ会員登録で全ての
メルマガ会員登録で全ての